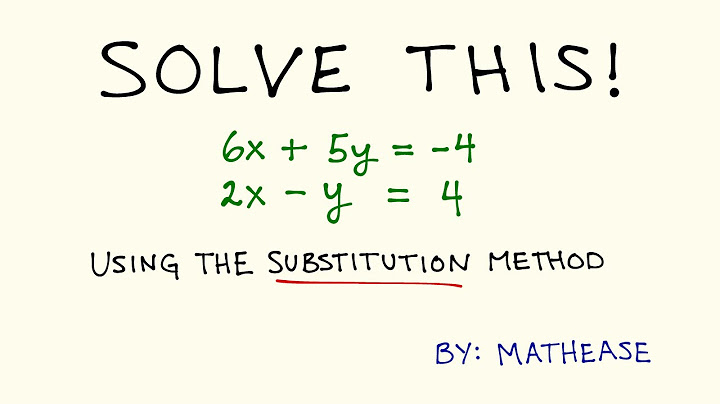Solving systems of equations by substitution answer key

To understand solving systems of equations by substitution, let’s first think about what substitution means.

We usesubstitution in many situations. First, when the pitcher on a softball team hurts her shoulder, another player can take her place as a substitute. Next, we can substitute vegan alternatives to animal products in a recipe. Finally, when we run into construction on our drive home and take a different road, we’re substituting one route for another. In each of these examples of substitution, we are replacing one entity with another equivalent one to solve a problem or reach a goal.

In the study of Algebra, we learn how to substitute variables for mathematical values in expressions. There is an algebraic property of equality called the Substitution Property, which states:

If x=y, then x may be replaced by y in expressions and equations. 

For example, we can substitute 7 for x in the following equation.

5+2=x

We can do this because 5+2=7.

The equation above has only one variable. What about situations where we have two or more variables and two or more equations? These systems of equations can seem more challenging, but solving systems of linear equations by substitution is often the easiest way to find solutions. 

Solving Systems of Equations Algebraically

There are multiple methods for solving systems of equations, including solving systems algebraically. Solving systems algebraically involves manipulating the equations we are given to uncover the values of each of the variables. 

But when must a system of linear equations be solved algebraically? When solving systems of equations, we should generally choose the method that takes the least effort and leaves the least room for error.

Let’s look at the system of linear equations below:

x=4

y+x=12

First, notice we are given the value of one of the variables, x. So, we can easily substitute that value for x into the other equation and solve for y. 

To review how to solve equations, check out our post: Solving One-Step Equations.

When we practice solving systems of equations, students are often told which method to use to find the solution. The directions might say: solve by graphing, solve by elimination, or solve by substitution. We will cover the first two methods in other posts. Here, we will focus on how to solve a system of equations algebraically using substitution.

How to Solve a System of Equations by Substitution

To solve a system of equations by substitution, we can rewrite a two-variable equation as a single variable equation by substituting the value of a variable from one equation into the other.

Let’s start by solving the system of equations that we looked at above:

x=4

y+x=12

As we decide how to solve systems of equations with substitution, we almost always have options. We have to decide which variable to substitute and which equation to substitute it into. 

In this example, the choice is clear. Since the first equation says that x=4, we will substitute x with 4 in the second equation so that the second equation becomes:

y+{\color{red}{4}}=12

Next, we can use the subtraction property of equality to subtract 4 from each side of the equation: 

y+4{\color{red}{-4}}=12{\color{red}{-4}}

y=8

We just solved this system of linear equations with substitution! The solution to this system is (4,8).

Knowing that the solution to a system of linear equations is the point of intersection, we can confirm graphically that the coordinate pair (4,8) is the solution to this system of equations.

Pro Tip: Online graphing calculators like Desmos can help you check your work quickly and easily.

Solving Systems of Equations by Substitution Steps

So, the steps for using the substitution method to solve a system of linear equations are:

1. Rewrite one of the equations to isolate one variable.
2. In the other equation, substitute the value of your isolated variable in for that variable.
3. Solve this second equation for the other variable. You should have a numerical value.
4. Substitute your numerical value into one of the two original equations and solve for the other variable.
5. Check your work. You can do this by graphing or by substituting the solutions into the original equations.

Substitution Method Examples

It’s helpful to use these steps when we consider how to solve systems of equations by substitution. Now, we can apply these steps to various systems to see if they work.

Solving Systems of Equations by Substitution Examples (One Solution)

Let’s see if these steps work for another system of equations:

x+y=10

x-y=2

1. Rewrite one of the equations to isolate one variable. Let’s solve the first equation for y:

x+y=10

x+y{\color{red}{-x}}=10{\color{red}{-x}}

y=10-x

2. In the other equation, substitute the value of your isolated variable in for that variable. So, we will substitute 10-x in for y into the second equation so that it becomes:

x-{\color{red}{(10-x)}}=2

3. Solve this second equation for the other variable. In this case, we are solving for x:

x-(10-x)=2

x-10+x=2

2x-10=2

2x-10{\color{red}{+10}}=2{\color{red}{+10}}

2x=12

x=6

4. Substitute your numerical value into one of the two original equations and solve for the other variable. We’ll substitute 6 for x into the first equation and solve for y.

{\color{red}{6}}+y=10

6+y{\color{red}{-6}}=10{\color{red}{-6}}

y=4

5. Check your work either. This time, we’ll confirm algebraically that the coordinate pair ({\color{red}{6}},{\color{blue}{4}}) works by substituting those values into the other equation, x-y=2:

{\color{red}{6}}-{\color{blue}{4}}=2

2=2

Solving Systems of Equations by Substitution Examples (No Solution)

The systems of equations we have solved so far had one solution, but systems of equations may also have zero, multiple, or an infinite number of solutions. Let’s solve a no solution system of equations by substitution:

x+y=3

y=-x+1

Notice that y is isolated in the second equation. So, we can substitute (-x+1) for y into the first equation so that it becomes: 

x+{\color{red}{(-x+1})}=3

1=3

At this point, we have a statement that is not true. A false statement tells us that there is no solution to the system of equations.

If we graph this system, we will see that these are equations of parallel lines, and parallel lines never intersect.

Solving Systems of Equations by Substitution Examples (Infinite Solutions)

Let’s solve another system of linear equations by substitution:

-y=x-4

2x+2y=8

In this system, the first equation almost has y isolated, so let’s rewrite that one:

-y=x-4

{\color{red}{-1}}(-y)={\color{red}{-1}}(x-4)

y=-x+4

Now we can substitute -x+4 for y in the second equation and solve algebraically:

2x+2{\color{red}{(-x+4)}}=8

2x-2x+8=8

8=8

Our equation is a true statement. However, it doesn’t tell us the values of our variables. Therefore, there are an infinite number of solutions to this system of equations. How can that be? Both equations graph as the same line. We can verify this by rewriting each equation into slope-intercept form.

Earlier, we found that the first equation can be rewritten as:

y=-x+4

Next, the second equation becomes:

2x+2y=8

\dfrac{2x+2y}{{\color{red}{2}}}=\dfrac{8}{{\color{red}{2}}}

x+y=4

x+y{\color{red}{-x}}={\color{red}{-x}}+4

y=-x+4

Since the equations are the same, the lines fully overlap. So, the system will have an infinite number of solutions because there are an infinite number of coordinate pairs that lie on both lines.

The Substitution Method: Keys to Remember

• Substitution is a helpful strategy in both life and math.
• Solving systems of equations algebraically involves using the Properties of Algebra.
• Substitution may be the obvious way to approach a system of equations, or question directions may require using substitution to solve systems of linear equations.
• Substitution allows us to eliminate one variable in a two-variable equation and solve for the other. 
• Once the value of one variable is determined, we can use substitution again to solve for the other variable(s).
• Systems of equations may have zero, one, multiple, or infinite solutions which can be determined and checked algebraically.

How do you solve linear equations with two variables using substitution?

What are the steps to solving a system of equations by elimination?